基础的数学知识

前言

说来实在是丢人，最近刷题发现自己连最简单的等差数列公式都忘记了... 也怪自己每次考数学都只是硬记公式，从来没有想过这些公式是如何推导出来的。 所以这里专门开记录一下学习的常用公式是如何得到的，以及如何在计算机中使用

等差数列的求和

在计算之前，首先我们需要明白数列是什么，数列是由一串常数组成的序列，既然是序列，它就有先后的顺序关系。如果数列中的连续的两项之间都相差一个固定的常数值，这个数列便被称之为等差数列。

举 3 个例子：

（1）：1、2、3、…、n （公差为 1）
（2）：2、4、6、…、n （公差为 2）
（3）：4、2、0、…、n （公差为 -2）

等差数列的求和怎么计算呢？一般使用如下两个公式（注意是 $a_1$）

$S_n = n * (a_1 + a_n) \div 2$

$S_n = n * a_1 + n * (n - 1) * d \div 2$

公式是对的，但是这是怎么来的呢？

如下图所示：

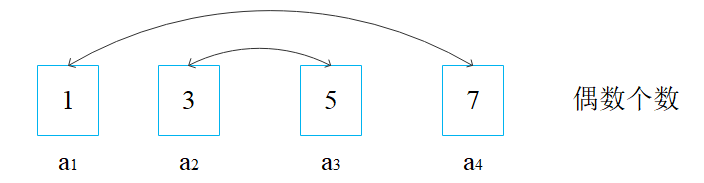
我们可以得出下面这个规律：

$a1 + a4 = a3 + a4$

按照这个规律，对于有 n 项（n 为偶数）的等差数列来说，一共有 $n/2$ 组 $a1 + a2$ 这样的组合，由此可以推出第一条公式

但是对于奇数个数的数列，按照上面的方法来计算的话，便会残留中间那一项，如下图所示：

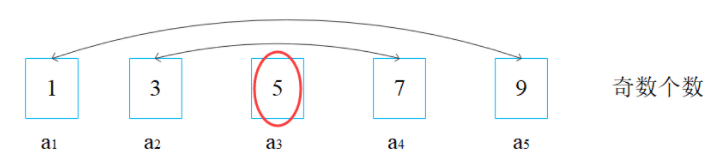
但这不是问题，除去中间那一项我们依旧可以按照这个公式计算，只需要做一点小的改动：（n 是指 n 项）

$S_{n-1} = (n-1) * (a_a + a_b) \div 2$

$S_{n-1}$ 表示除去中间那项

中间那一项我们可以这样计算得到：

$a_{\frac{a + b}{2}} = \frac{a_a + a_b}{2}$

于是乎，我们将上面两条相加，便得到了上述中的一式。

$S_n = n * (a_a + a_b) \div 2$

例如求 2 ... 5 的和
n = 4
Sn = 4 * (2 + 5) / 2 = 14

例如求 3 ... 5 的和
n = 3
Sn = 3 * (3 + 5) / 2 = 12

// n = (high - low + 1)
int cur = (high - low + 1) * (low + high) / 2;

如何理解对数

在学习算法时，经常能用到 $Log(n)$ 来表示算法的变化情况，那这个对数是啥呢？

放两张图方便快速回忆：

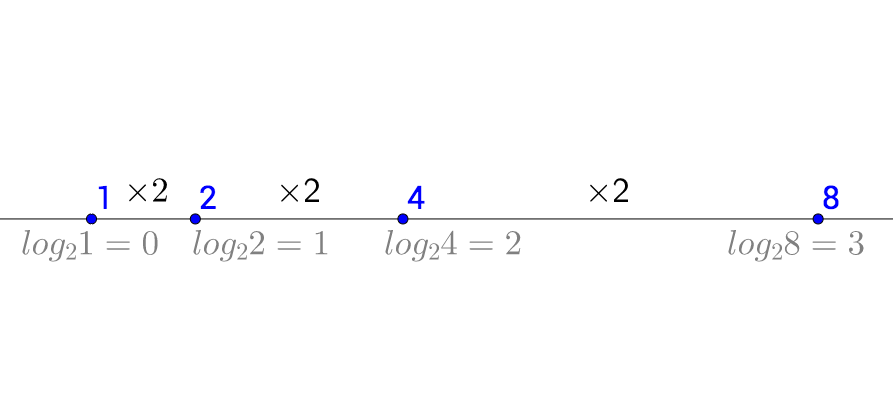
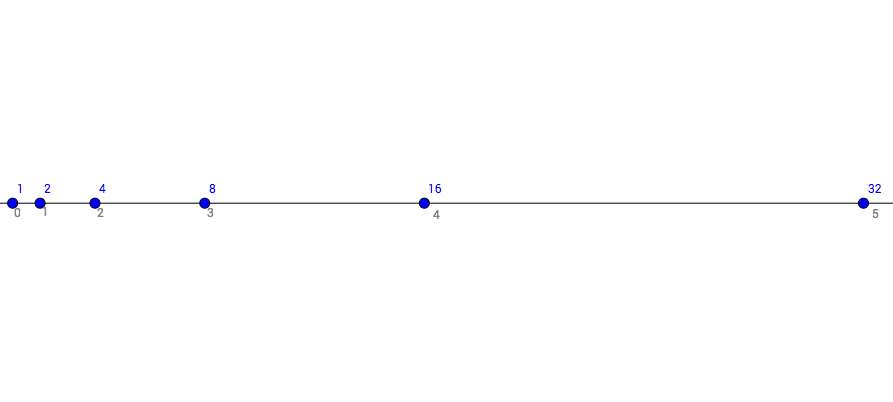
更多细节参考：如何理解「对数」？ - 马同学的回答 - 知乎

复数是什么？

当我们探讨复数时，我们可以采用一个形象的比喻来解释。想象一个数学世界，有两个维度：一个是实部维度，另一个是虚部维度。在这个世界中，每个点都由实部和虚部组成，就像在二维平面上的坐标点一样。

想象你站在一个平面上，实部维度是水平方向，虚部维度是垂直方向。如果你只考虑实数，你只能在水平方向上移动，就像在一条直线上。但如果你引入虚数，就像给你一对翅膀，你可以在垂直方向上飞翔。

复数就是这个数学世界中的点。每个复数都可以用一个实部和一个虚部表示。例如，复数 $3 + 2i$ 可以想象成你站在 $3$ 这个点的水平位置，并向上飞了 $2$ 个单位。这就是复数的本质：它们不仅有大小（通过模），还有方向（通过辐角）。

在这个比喻中，实部就是你在平面上的水平位置，虚部就是你在平面上的垂直位置。复数的加法就像在平面上移动两个点，复数的乘法就像将两个点相对于原点进行旋转和拉伸。

即，复数是一个引入了两个维度的数学世界，让我们可以在实部和虚部的维度上自由地操作，以解决实际问题，包括那些实数难以解决的问题。

      Imaginary
         ^
         |
         |      b
         |     /
         |    /  
         |   /    
         |  /      
         | /       
         |/        
---------+--------> Real
         |

在这个图中：

• 复平面仍然是一个笛卡尔坐标系，横轴表示实轴（Real Axis），纵轴表示虚轴（Imaginary Axis）。
• 复数 $a + bi$ 被表示为从原点出发的矢量，矢量的水平分量 $a$ 对应实部，垂直分量 $b$ 对应虚部。
• 实部 $a$ 决定了矢量在实轴上的位置，虚部 $b$ 决定了矢量在虚轴上的位置。
• 矢量的模（长度）为 $\sqrt{a^2 + b^2}$，表示复数的大小。
• 矢量与正实轴的夹角为辐角（角度）$\theta$，可以通过三角函数计算。

希望这个图示更加清晰地表达了复数的概念。虽然这个图示只是一个简化的表示，但应该能够帮助您获得关于复数的更好的直观理解。

虚部和实部是什么？

虚部和实部是用来描述复数的两个组成部分。复数是由实部和虚部组成的，形式为 $a + bi$，其中 $a$ 是实部，$b$ 是虚部，而 $i$ 是虚数单位，满足 $i^2 = -1$。

具体来说：

1. 实部（Real Part）： 实部是复数的实数部分，即在复数 $a + bi$ 中的 $a$ 部分。实部表示复数在实轴上的投影，也就是复数在水平方向上的位置。

2. 虚部（Imaginary Part）： 虚部是复数的虚数部分，即在复数 $a + bi$ 中的 $b$ 部分。虚部表示复数在虚轴上的投影，也就是复数在垂直方向上的位置。

举个例子，考虑复数 $3 + 2i$。在这个复数中，实部是 $3$，虚部是 $2$。这意味着复数位于实轴上 $3$ 的位置，同时在虚轴上向上飞翔了 $2$ 个单位。

实部和虚部的概念使我们能够在复平面（也称为复数平面）上表示和操作复数。复平面是一个二维平面，横轴是实轴，纵轴是虚轴，每个复数在复平面上都对应一个点。通过实部和虚部，我们可以了解复数的大小（通过模）和方向（通过辐角），并进行复数的加法、减法、乘法等操作。

  Imaginary Axis
       ^
       |
       b----- a + bi  
       |     | 
       |     | 
       |     | 
-------+-----a---> Real Axis
       |      
       |       
       |       
       |       

在这个图中：

• 复平面是一个笛卡尔坐标系，横轴表示实轴（Real Axis），纵轴表示虚轴（Imaginary Axis）。
• 复数 $a + bi$ 被表示为一个点在复平面上的位置。点的水平坐标 $a$ 对应实部，垂直坐标 $b$ 对应虚部。
• 实部 $a$ 决定了复数在实轴上的位置。
• 虚部 $b$ 决定了复数在虚轴上的位置。

希望这次的描述和图示能够更清晰地表达复平面、实部和虚部的概念。

虚数是什么？

虚数是一种特殊类型的数，用来表示负数的平方根，形式为 $bi$，其中 $b$ 是一个实数，而 $i$ 是虚数单位，满足 $i^2 = -1$。虚数单位 $i$ 是一个虚拟的数学概念，它没有在实数范围内的实际对应，但它的引入在解决一些问题时非常有用。

虚数的引入主要是为了解决以下几个问题：

1. 负数的平方根问题： 在实数范围内，负数的平方根是没有实数解的。例如，方程 $x^2 = -1$ 没有实数解。虚数单位 $i$ 的引入允许我们在数学上表示负数的平方根，即 $\sqrt{-1}$。

2. 复数的表示： 复数是实部和虚部的组合，形式为 $a + bi$，其中 $a$ 和 $b$ 都是实数。复数可以用来表示许多实际问题中的量，包括振动、波动、电磁场等。

3. 解决多项式方程： 虚数在解决多项式方程时非常有用，特别是对于高阶多项式。虚数的引入扩展了解方程的范围，使得一些看似无解的问题变得有解。

4. 工程和物理应用： 虚数在工程学和物理学中有广泛的应用，例如交流电路分析、振动系统建模、量子力学等领域。复数在这些领域中可以非常方便地描述相位、幅度和周期性变化等现象。

虽然虚数在初始引入时可能会让人感到抽象和奇怪，但它们在解决实际问题中具有实质性的作用。虚数是复数的一个重要组成部分，而复数则是更广泛数学和科学领域中的基础。

积分是什么？

积分是数学中的一个基本概念，它表示对一个函数的某种性质在一个给定区间内的累积或总和。积分的主要目的是测量曲线下的面积，描述变化率，求解方程等。

具体来说，积分可以有不同的含义和用途，主要分为以下两种常见类型：

1. 不定积分：不定积分通常用于找到一个函数的原函数，也称为不定积分的结果。原函数是指一个函数的导数，因此不定积分可以看作是导数的逆运算。不定积分的结果通常包含一个常数项，因为导数无法确定原函数的常数部分。

   例如，如果我们有一个函数 $f(x)$，它的不定积分表示为 $\int f(x) dx$，则结果是一个函数 $F(x)$，其中 $F'(x) = f(x)$，即 $F(x)$ 是 $f(x)$ 的一个原函数。

2. 定积分：定积分用于计算一个函数在一个特定区间内的累积效应或总和，通常表示为 $\int_a^b f(x) dx$，其中 $a$ 和 $b$ 是积分的上下限。定积分的结果是一个数值，表示在区间 $[a, b]$ 内的面积或其他性质。

   例如，如果我们有一个函数 $f(x)$，我们可以使用定积分来计算该函数在区间 $[a, b]$ 内的面积，这个面积表示为 $\int_a^b f(x) dx$。

积分在数学中有广泛的应用，包括解决微积分问题、计算曲线下的面积、描述物理过程中的累积效应、计算概率分布下的期望值等。它是数学和科学领域中不可或缺的工具之一。

$\int$ 和 $\sum$ 的区别

$\int$ 和 $\sum$ 是两个在数学中表示累积或总和的符号，但它们用于不同类型的数量和不同背景的数学概念，因此具有一些关键区别：

1. 用途：

   • $\int$ 表示积分，用于测量曲线下的面积、计算变化率、求解方程等连续性的操作。积分通常用于处理连续函数或曲线。
   • $\sum$ 表示求和，用于对离散集合中的元素进行累积操作。求和通常用于处理离散数据、序列、级数等。

2. 数学对象：

   • $\int$ 通常与连续函数相关，用于对函数在一个区间内的积分，结果是一个数值或函数。
   • $\sum$ 通常与离散序列或集合相关，用于对序列或集合中的元素进行累积求和，结果是一个数值。

总之，$\int$ 和 $\sum$ 分别用于处理不同类型的数量和数学概念，$\int$ 用于连续性的操作和函数，而 $\sum$ 用于离散性的操作和集合或序列。它们在数学中具有不同的应用和含义。

求不定积分

求不定积分是找到一个函数的原函数（也称为不定积分的结果）。原函数是指一个函数的导数，因此不定积分可以看作是导数的逆运算。下面举例说明如何求不定积分以及不定积分与导数之间的关系。

考虑函数 $f(x) = 2x$，我们想求它的不定积分 $\int f(x) dx$。

步骤 1：写出不定积分的表达式。不定积分的一般形式为 $\int f(x) dx$，其中 $f(x)$ 是被积函数，$x$ 是积分变量。

$\int 2x dx$

步骤 2：计算不定积分。要计算这个不定积分，我们可以使用幂的不定积分公式。对于 $x^n$ 形式的函数，不定积分的结果是 $\frac{1}{n+1} x^{n+1}$，其中 $n$ 不等于 -1。

在我们的例子中，$n = 1$，所以：

$\int 2x dx = 2 \cdot \frac{1}{2} x^{2} + C$

步骤 3：添加常数项。不定积分结果中通常包含一个常数项 $C$，因为导数无法确定原函数的常数部分。

$2 \cdot \frac{1}{2} x^{2} + C = x^{2} + C$

所以，不定积分 $\int 2x dx$ 的结果是 $x^2 + C$，其中 $C$ 是常数。

关于不定积分和导数的关系：

• 不定积分是导数的逆运算。如果 $F(x)$ 是函数 $f(x)$ 的一个原函数（即 $F'(x) = f(x)$），那么 $\int f(x) dx = F(x) + C$，其中 $C$ 是常数。这意味着如果我们对 $F(x)$ 求导，将会得到 $f(x)$。

• 在上面的例子中，我们求得不定积分 $\int 2x dx = x^2 + C$，如果我们对 $x^2 + C$ 求导，将会得到 $2x$，即原来的函数 $f(x) = 2x$。

• 常数 $C$ 是积分常数，因为不定积分结果包含无法确定的常数项。不同的原函数可能会有不同的常数项，但它们的导数是相同的。

不定积分在微积分中用于解决各种问题，包括计算曲线下的面积、求解微分方程、估计累积效应等。

对数 $\log$ 是什么？

对数是一种数学运算，用于解决指数运算的逆问题。具体来说，如果 $b^x = a$，其中 $a$ 和 $b$ 是正实数且 $b$ 不等于 $1$，那么 $x$ 称为以 $b$ 为底数的 $a$ 的对数，通常用 $\log_b(a)$ 表示。对数的一般定义如下：

$$\log_b(a) = x \quad \text{当且仅当} \quad b^x = a$$

这里，$b$ 被称为底数，$a$ 被称为真数，$x$ 被称为对数。

举个具体的例子：

1. 以 10 为底的对数：$\log_{10}(100) = 2$，因为 $10^2 = 100$。这表示 $100$ 的以 $10$ 为底的对数等于 $2$。

2. 以 2 为底的对数：$\log_{2}(8) = 3$，因为 $2^3 = 8$。这表示 $8$ 的以 $2$ 为底的对数等于 $3$。

3. 以 e 为底的对数：$\log_{e}(e^3) = 3$，因为 $e^3 = e^3$。这表示 $e^3$ 的以 $e$ 为底的对数等于 $3$。

对数的一个重要特性是它可以将指数运算转化为乘法运算。例如，如果 $\log_b(a) = x$，那么 $b^x = a$，这意味着以 $b$ 为底的对数运算可以用来解决指数方程。

对数在数学、科学、工程、计算机科学等领域都有广泛的应用。它常用于测量数量级、表示倍数关系、解决复杂的增长和衰减问题，以及简化复杂计算。

Reference

• 你应该想想，等差数列的求和是怎么来的？