跳到主要内容

动态规划学习-理论部分

转载自 牛逼了，原来大神都是这样学动态规划的…

什么是动态规划？​

动态规划（dynamic programming，简称 dp）是一种多阶段决策最优解模型，一般用来求最值问题，多数情况下它可以采用自下而上的递推方式来得出每个子问题的最优解（即最优子结构），进而自然而然地得出依赖子问题的原问题的最优解。

划重点： 1、多阶段决策，意味着问题可以分解成子问题，子子问题....，也就是说问题可以拆分成多个子问题进行求解

2、最优子结构，在自下而上的递推过程中，我们求得的每个子问题一定是全局最优解，既然它分解的子问题是全局最优解，那么依赖于它们解的原问题自然也是全局最优解。

3、自下而上，怎样才能自下而上的求出每个子问题的最优解呢，可以肯定子问题之间是有一定联系的，即迭代递推公式，也叫「状态转移方程」，要定义好这个状态转移方程， 我们就需要定义好每个子问题的状态（DP 状态），那为啥要自下而上地求解呢，因为如果采用像递归这样自顶向下的求解方式，子问题之间可能存在大量的重叠，大量地重叠子问题意味着大量地重复计算，这样时间复杂度很可能呈指数级上升（在下文中我们会看到多个这样重复的计算导致的指数级的时间复杂度），所以自下而上的求解方式可以消除重叠子问题。

简单总结一下，最优子结构，状态转移方程，重叠子问题就是动态规划的三要素，这其中定义子问题的状态与写出状态转移方程是解决动态规划最为关键的步骤，状态转移方程如果定义好了，解决动态规划就基本不是问题了。

解题步骤​

既然我们知道动态规划的基本概念及特征，那么怎么判断题目是否可以用动态规划求解呢？

其实也很简单，当问题的定义是求最值问题，且问题可以采用递归的方式，并且递归的过程中有大量重复子问题的时候，基本可以断定问题可以用动态规划求解，于是我们得出了求解动态规划基本思路如下（解题四步曲）

  1. 判断是否可用递归来解，可以的话进入步骤 2
  2. 分析在递归的过程中是否存在大量的重复子问题
  3. 采用备忘录的方式来存子问题的解以避免大量的重复计算（剪枝）
  4. 改用自底向上的方式来递推，即动态规划

可能不少人看了以上的动态规划的一些介绍还是对一些定义如 DP 状态，状态转移方程，自底而上不了解，没关系 ，接下来我们会做几道习题来强化一下大家对这些概念及动态规划解题四步曲的理解，每道题我们都会分别用递归，递归+备忘录，动态规划来求解一遍，这样也进一步帮助大家来巩固我们之前学的递归知识

入门题：斐波那契数列​

接下来我们来看看怎么用动态规划解题四步曲来解斐波那契数列

画外音：斐波那契数列并不是严格意义上的动态规划，因为它不涉及到求最值，用这个例子旨在说明重叠子问题与状态转移方程

使用递归的方法​

判断是否可用递归来解 显然是可以的，递归代码如下

public static int fibonacci(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

分析在递归的过程中是否存在大量的重复子问题，怎么分析是否有重复子问题？画出递归树

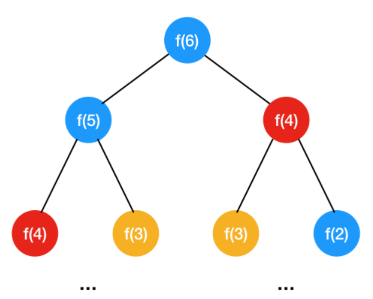
可以看到光是求 f(6)f(6) ,就有两次重复的计算, f(4)f(4) 求解了两次, f(3)f(3) 求解了两次

时间复杂度是指数级别，递归时间复杂度怎么看，解决每个子问题需要的时间乘以子问题总数，每个子问题需要的时间即 f(n)=f(n−1)+f(n−2)f(n) = f(n-1) + f(n-2) 即只做了一次加法运算，子问题的个数有多少呢？

因为每个问题一分为二，是个二叉树，可以看到第一层 1 个，第二层 2 个，第三层 4 个，即 1+2+22+...2n1 + 2 + 2^2 + ...2^n ,所以总的来说时间复杂度是 O(2n)O(2^n) ,是指数级别

画外音：求解问题 f(6)f(6) ,转成求 f(5),f(4)f(5),f(4) ,从原问题出发，分解成求子问题，子问题再分解成子子问题….，直到再也不能分解，这种 从原问题展开子问题进行求解的方式叫自顶向下

使用备忘录避免重复计算（剪枝）​

采用备忘录的方式来存子问题的解以避免大量的重复计算既然以上中间子问题中存在着大量的重复计算，那么我们可以把这些中间结果给缓存住（可以用哈希表缓存），如下

public static int fibonacci(int n) {
    if (n = 1) return 1;
    if (n = 2) return 2;
    if (map.get(n) != null)  {
        return map.get(n);
    }
    int result = fibonacci(n - 1) + fibonacci(n - 2);
    map.put(n, result);
    return result;
}

这么缓存之后再看我们的递归树

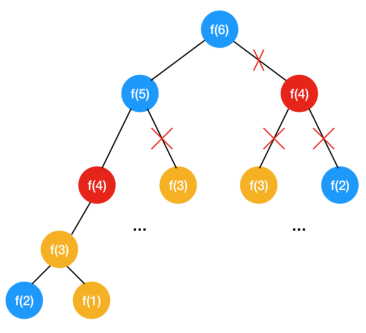
可以看到通过缓存中间的数据，做了大量地剪枝的工作，同样的 f(4),f(3),f(2)f(4),f(3),f(2) ,都只算一遍了,省去了大量的重复计算，问题的规模从二叉树变成了单链表（即 n），时间复杂度变成了 O(n)O(n) ,不过由于哈希表缓存了所有的子问题的结果，空间复杂度是 O(n)O(n) 。

使用动态规划​

改用自底向上的方式来递推，即动态规划 我们注意到如下规律：

f(1) = 1
f(2) = 2
f(3) = f(1) + f(2) = 3
f(4) = f(3) + f(2) = 5
....
f(n) = f(n-1) + f(n-2)

可以发现从 f(3)f(3) 开始每项都是上两项的相加结果

所以只要依次自底向上求出 f(3),f(4),…f(3),f(4),… ,自然而然地就求出了 f(n)f(n)

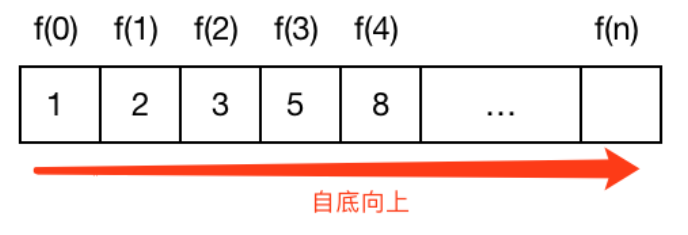
画外音：从最终地不能再分解的子问题根据递推方程 f(n)=f(n−1)+f(n−2)f(n) = f(n-1) + f(n-2) 逐渐求它上层的问题，上上层问题，最终求得一开始的问题，这种求解问题的方式就叫自底向上。

f(n)f(n) 就是定义的每个子问题的状态（DP 状态）, f(n)=f(n−1)+f(n−2)f(n) = f(n-1) + f(n-2) 就是状态转移方程，即 f(n)f(n) 由 f(n−1),f(n−2)f(n-1), f(n-2) 这两个状态转移而来,由于每个子问题只与它前面的两个状态，所以我们只要定义三个变量，自底向上不断循环迭代即可，如下

public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;

    int result = 0;
    int pre = 1;
    int next = 2;
    
    // 从 3 开始自底向上
    for (int i = 3; i < n + 1; i ++) {
        result = pre + next;
        pre = next;
        next = result;
    }
    return result;
}

这样时间复杂度虽然还是 O(n)O(n) ,但空间复杂度只由于只定义了三个变量（result、pre、next）所以是常量 O(1)O(1) 。

通过简单地斐波那契的例子，相信大家对自底向上，DP 状态， DP 转移方程应该有了比较深入地认识，细心的同学一定发现了最优子结构怎么没有，因为前面我们也说了，斐波那契数列并不是严格意义上的动态规划，只是先用这个简单地例子来帮助大家了解一下一些基本的概念。在之后的习题中我们将会见识到真正的动态规划

小试牛刀：三角形的最小路径和​

注意：仔细看图，这不是二叉树，它就是一个三角形

如图示，以上三角形由一连串的数字构成，要求从顶点 2 开始走到最底下边的最短路径，每次只能向当前节点下面的两个节点走，如 3 可以向 6 或 5 走，不能直接走到 7。

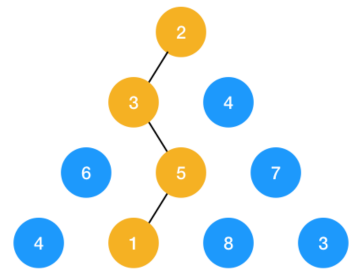
如图示：从 2 走到最底下最短路径为 2+3+5+1=112 + 3 + 5 + 1 = 11 ,即为我们所求的

首先我们需要用一个二维数组来表示这个三个角形的节点，用二维数组显然可以做到， 第一行的 2 用 a[0][0] 表示，第二行元素 3，4 用 a[1][0]，a[1][1]，依此类推。（因为它不是二叉树，所以可以使用二维数组的一半表示它）

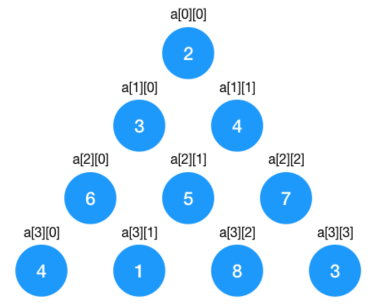
定义好数据结构之后，接下来我们来看看如何套用我们的动态规划解题套路来解题

使用递归的方式​

如果用递归，就要穷举所有的路径和，最后再求所有路径和的最小值，我们来看看用递归怎么做。

对于每个节点都可以走它的左或右节点，假设我们定义 traverse(i, j) 为节点 a[i][j] 下一步要走的节点，则可以得出递归公式的伪代码如下

traverse(i, j) = {
    traverse(i + 1, j);        // 向节点 i,j 下面的左节点走一步
    traverse(i + 1, j + 1);    // 向节点 i,j 下面的右节点走一步
}

什么时候终止呢，显然是遍历到三角形最后一条边的节点时终止，发现了吗？

对每个节点来说，在往下（无论是往左还是往右）遍历的过程中，问题规模不断地在缩小，也有临界条件（到达最后一条边的节点时终止），分解的子问题也有相同的解决问题的思路（对于每个节点的遍历都是往左或往右），符合递归的条件！

于是我们得到递归代码如下：

// 因为它不是二叉树，所以可以使用二维数组的一半表示它
private static int[][] triangle = {
            {2, 0, 0, 0},
            {3, 4, 0, 0},
            {6, 5, 7, 0},
            {4, 1, 8, 3}
};

public static int traverse(int i, int j) {
    int totalRow = 4; // 总行数
    if (i >=  totalRow - 1) {
        return 0;
    }
    // 往左下节点走时
    int leftSum = traverse(i+1, j) + triangle[i+1][j]; // 子节点最小值加上当前值
    // 往右下节点走时
    int rightSum = traverse(i+1, j+1) + triangle[i+1][j+1];
    // 记录每个节点往左和往右遍历的路径和的最小值
    return Math.min(leftSum, rightSum);
}

public static  void main(String[] args)  throws Throwable {
    int sum = traverse(0, 0) + triangle[0][0];
    System.out.println("sum = " + sum);
}

时间复杂度是多少呢，从以下伪代码可以看出

traverse(i, j) = {
    traverse(i + 1, j);        // 向节点 i,j 下面的左节点走一步
    traverse(i + 1, j + 1);    // 向节点 i,j 下面的右节点走一步
}

对于每个节点，要么向左或向右，即每个问题都分解成了两个子问题，和斐波那契数列一样，如果画出递归树也是个二叉树，所以时间复杂度是 O(2n)O(2^n) ,也是指数级别。

分析是否存在重复子问题​

分析在递归的过程中是否存在大量的重复子问题

为啥时间复杂度是指数级别呢，我们简单分析一下：

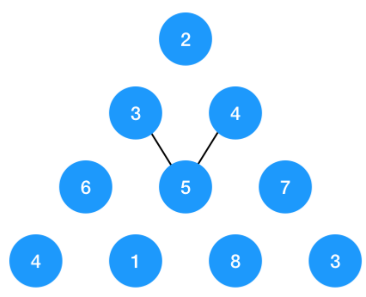
对于节点 3 和 4 来说，如果节点 3 往右遍历， 节点 4 往左遍历，都到了节点 5，节点 5 往下遍历的话就会遍历两次，所以此时就会出现重复子问题

采用备忘录避免重复计算（剪枝）​

既然出现了，那我们就用备忘录把中间节点缓存下来

于是我们的代码改为如下所示

private static int[][] triangle = {
            {2, 0, 0, 0},
            {3, 4, 0, 0},
            {6, 5, 7, 0},
            {4, 1, 8, 3}
    };

// 记录中间状态的 map
private static HashMap<String, Integer> map = new HashMap();

public static int traverse(int i, int j) {
    String key = i + "" + j;
    if (map.get(key) != null) {
        return map.get(key);
    }

    int totalRow = 4; // 总行数
    if (i >=  totalRow - 1) {
        return0;
    }
    // 往左下节点走时
    int leftSum = traverse(i+1, j) + triangle[i+1][j];
    // 往右下节点走时
    int rightSum = traverse(i+1, j+1) + triangle[i+1][j+1];
    // 记录每个节点往左和往右遍历的路径和的最小值
    int result = Math.min(leftSum, rightSum);
    map.put(key, result);
    return result;
}

这么一来，就达到了剪枝的目的，避免了重复子问题，时间复杂度一下子下降到 O(n)O(n) ,空间复杂度呢，由于我们用哈希表存储了所有的节点的状态，所以空间复杂度是 O(n)O(n) 。

使用动态规划​

改用自底向上的方式来递推，即动态规划

重点来了，如何采用自底向上的动态规划来解决问题呢？

我们这么来看，要求节点 2 到底部边的最短路径，只要先求得节点 3 和 节点 4 到底部的最短路径值，然后取这两者之中的最小值再加 2 不就是从 2 到底部的最短路径了吗，同理，要求节点 3 或 节点 4 到底部的最小值，只要求它们的左右节点到底部的最短路径再取两者的最小值再加节点本身的值（3 或 4）即可。

我们知道对于三角形的最后一层节点，它们到底部的最短路径就是其本身，于是问题转化为了已知最后一层节点的最小值怎么求倒数第二层到最开始的节点到底部的最小值了。先看倒数第二层到底部的最短路径怎么求

同理，第二层对于节点 3 ，它到最底层的最短路径转化为了 3 到 7 或 6 节点的最短路径的最小值，即 9；而对于节点 4，它到最底层的最短路径转化为了 4 到 6 或 10 的最短路径两者的最小值，即 10。

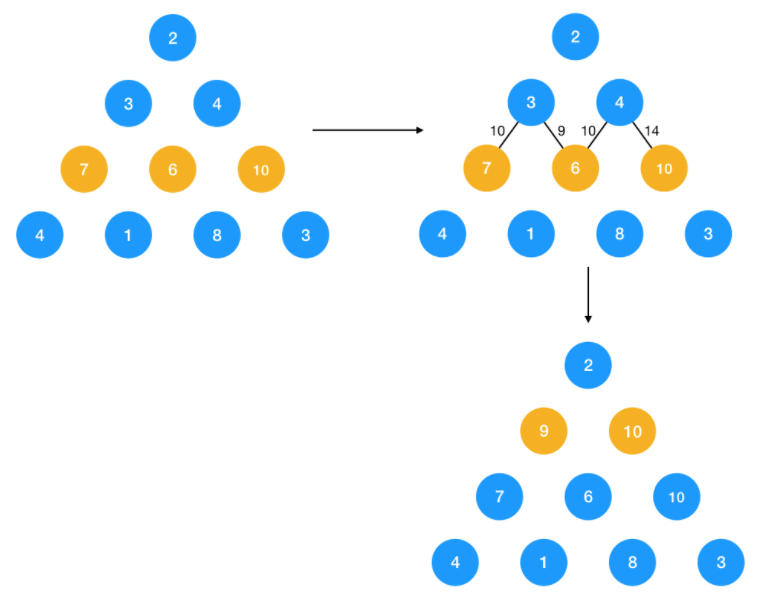
接下来要求 2 到底部的路径就很简单了，只要求 2 到节点 9 与 10 的最短路径即可，显然为 11。

于是最终的 11 即为我们所求的值，接下来我们来看看怎么定义 DP 的状态与状态转移方程。我们要求每个节点到底部的最短路径，于是 DP 状态 DP[i,j] 定义为 i，j 的节点到底部的最小值，DP状态转移方程定义如下：

DP[i,j] = min(DP[i+1, j], DP[i+1, j+1]) + triangle[i,j]

这个状态转移方程代表要求：节点到最底部节点的最短路径只需要求左右两个节点到最底部的最短路径两者的最小值再加此节点本身！

仔细想想我们上面的推导过程是不是都是按这个状态转移方程推导的，实在不明白建议多看几遍上面的推导过程，相信不难明白。

DP 状态 DP[i,j] 有两个变量，需要分别从下而上，从左到右循环求出所有的 i，j，而有了状态转移方程求出代码就比较简单了，如下：

private static int[][] triangle = {
        {2, 0, 0, 0},
        {3, 4, 0, 0},
        {6, 5, 7, 0},
        {4, 1, 8, 3}
};

public static int traverse() {
    int ROW = 4;
    // 这个 mini 等价于上面图的黄色部分，初始时这里取 triangle 二维数组的最后一行
    int[] mini = triangle[ROW - 1]; 

    // 从倒数第二行求起，因为最后一行的值本身是固定的
    for (int i = ROW - 2; i >= 0; i--) {
        for (int j = 0; j < triangle[j].length; j++) {
            mini[j] = triangle[i][j] + Math.min(mini[j], mini[j+1]);
        }
    }
    return mini[0];
}

public static  void main(String[] args)  throws Throwable {
    int minPathSum = traverse();
    System.out.println("sum = " + minPathSum);
}

可能有一些人对 mini 数组的定义有疑问，这里其实用了一个比较取巧的方式，首先我们定义 mini 的初始值为最后一行的节点，因为最后一行的每个节点的 DP[i,j] 是固定值，只要从倒数第二行求起即可，其次我们知道每个节点到底部的最短路径只与它下一层的 D[I+1,j], D[i+1, j] 有关，所以只要把每一层节点的 DP[i,j] 求出来保存到一个数组里即可，就是为啥我们只需要定义一下 mini 一维数组的原因

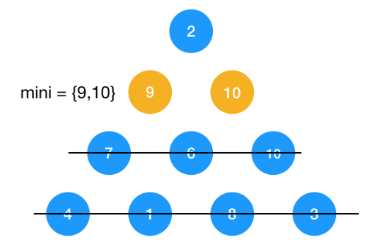
如图示：要求节点 2 到底部的最短路径，它只关心节点 9， 10，之前层数的节点无需再关心！因为 9，10 已经是最优子结构了，所以只保存每层节点（即一维数组）的最值即可！

这里我们再来谈谈 最优子结构，在以上的推导中我们知道每一层节点到底部的最短路径依赖于它下层的左右节点的最短路径，求得的下层两个节点的最短路径对于依赖于它们的节点来说就是最优子结构

最优子结构对于子问题来说属于全局最优解，这样我们不必去求节点到最底层的所有路径了，只需要依赖于它的最优子结构即可推导出我们所要求的最优解，所以最优子结构有两层含义

  • 一是它是子问题的全局最优解，依赖于它的上层问题只要根据已求得的最优子结构推导求解即可得全局最优解
  • 二是它有缓存的含义，这样就避免了多个依赖于它的问题的重复求解（消除重叠子问题）。

总结：仔细回想一下我们的解题思路，我们先看了本题是否可用递归来解，在递归的过程中发现了有重叠子问题，于是我们又用备忘录来消除递归中的重叠子问题，既然我们发现了 此问题可以用 递归 + 备忘录 来求解，自然而然地想到它可以用自底向上的动态规划来求解。

是的，求解动态规划就按这个套路来即可，最重要的是要找出它的状态转移方程，这需要在自下而上的推导中仔细观察。

进阶：凑零钱​

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例：

输入: coins = [1, 2, 5], amount = 11
输出: 3  
解释: 11 = 5 + 5 + 1 

输入: coins = [2], amount = 3
输出: -1

来套用一下我们的动态规划解题四步曲

使用递归的方法​

判断是否可用递归来解

对于 amount 来说，如果我们选择了 coins 中的任何一枚硬币，则问题的规模（amount）缩小了，再对缩小的 amount 也选择 coins 中的任何一枚硬币，直到再也不能选择

amount = 0 代表有符合条件的解，amount < 0 代表没有符合条件的解

从描述中我们可以看出问题可以分解成子问题，子问题与原问题具有相同的解决问题的思路，同时也有临界条件，符合递归的条件，由此可证可以用递归求解，接下来我们来看看，如何套用 递归四步曲 来解题

1、定义这个函数，明确这个函数的功能,函数的功能显然是给定一个 amount，用定义好的 coins 来凑，于是我们定义函数如下

private static int f(int amount, int[] coins) {
}

2、寻找问题与子问题的关系，即递推公式

这题的递推关系比较难推导，我们一起看下，假设 amount 为零钱， f(amount, coins) 为所需要的最少硬币数，当选中了coins 中的第一枚硬币之后（即为 coins[0]），则需再对剩余的 amount – coins[0] 金额求最少硬币数，即调用 f(amount – coins[0], coins)，由此可知当选了第一枚硬币后的递推公式如下

f(amount, coins) = f(amount-coins[0], coins) + 1  // 这里的 1 代表选择了第一枚硬币

如果选择了第二，第三枚呢，递推公式如下

f(amount, coins) = f(amount-coins[1], coins) + 1 // 这里的 1 代表选择了第二枚硬币
f(amount, coins) = f(amount-coins[2], coins) + 1 // 这里的 1 代表选择了第三枚硬币

我们的目标是求得所有以上 f(amount, coins) 解的的最小值，于是可以得到我们的总的递推公式如下

// 其中 i 的取值为 0 到 coins 的大小，coins[i] 表示选择了此硬币, 1 表示选择了coins[i]  这一枚硬币
f(amount, coins) = min{ f(amount - coins[i], coins) + 1 }

3、将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中

得出了递推公式用代码实现就简单了，来简单看一下

// 别忘了加上边界条件
public class Solution {

    private static int exchange(int amount, int[] coins) {

        // 说明零钱刚好凑完
        if (amount == 0) {
            return0;
        }

        // 说明没有满足的条件
        if (amount < 0) {
            return -1;
        }

        int result = Integer.MAX_VALUE;

        for (int i = 0; i < coins.length; i++) {
            int subMin = exchange(amount - coins[i], coins);
            if (subMin == -1) continue;
            result = Math.min(subMin + 1, result);
        }

        // 说明没有符合问题的解
        if (result == Integer.MAX_VALUE) {
            return -1;
        }

        return result;
    }

    public static  void main(String[] args)  throws Throwable {
        int amount = 11;
        int[] coins = {1,2,5};
        int result = exchange(amount, coins);
        System.out.println("result = " + result);
    }
}

剪枝操作​

计算时间复杂度 这道题的时间复杂度很难看出来，一般看不出来的时候我们可以画递归树来分析，针对 amount = 11 的递归树 如下

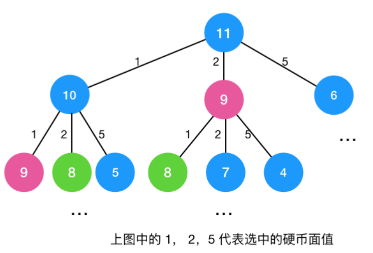
前文我们说到斐波那契的递归树是一颗二叉树，时间复杂度是指数级别，而凑零钱的递归树是一颗三叉树，显然时间复杂度也是指数级别!

分析在递归的过程中是否存在大量的重叠子问题（动态规划第二步）

由递归树可知，存在重叠子问题，上一节中的 9、8，都重复算了，所以存在重叠子问题！

既然我们知道存在重叠子问题，那么就可以用备忘录来存储中间结果达到剪枝的目的

public class Solution {

    // 保存中间结果
    private static HashMap<Integer, Integer> map = new HashMap();

    // 带备忘录的递归求解
    private static int exchangeRecursive(int amount, int[] coins) {
        if (map.get(amount) != null) {
            return map.get(amount);
        }

        // 说明零钱已经凑完
        if (amount == 0) {
            return0;
        }

        // 说明没有满足的条件
        if (amount < 0) {
            return -1;
        }

        int result = Integer.MAX_VALUE;
        for (int i = 0; i < coins.length; i++) {
            int subMin = exchangeRecursive(amount - coins[i], coins);
            if (subMin == -1) continue;
            result = Math.min(subMin + 1, result);
        }

        // 说明没有符合问题的解
        if (result == Integer.MAX_VALUE) {
            return -1;
        }

        map.put(amount, result);
        return result;
    }

    public static  void main(String[] args)  throws Throwable {
        int amount = 11;
        int[] coins = {1,2,5};
        int result = exchangeRecursive(amount, coins);
        System.out.println("result = " + result);
    }
}

使用动态规划​

参考资料 基本动态规划之硬币问题

这里修改下硬币的面值：1 元，3 元，5 元的硬币若干（无限），现在需要凑出 11 元，问如何组合才能使硬币的数量最少？

前面我们推导出了如下递归公式

// 其中 i 的取值为 0 到 coins 的大小，coins[i] 表示选择了此硬币, 1 表示选择了coins[i]  这一枚硬币
f(amount, coins) = min{ f(amount - coins[i], coins) + 1 }

从以上的递推公式中我们可以获取 DP 的解题思路，我们定义 DP(i) 为凑够零钱 i 需要的最小值，状态转移方程如下

// 其中 j 的取值为 0 到 coins.length 的大小，
// i 代表取了 coins[j] 这一枚硬币。
DP[i] =  min{ DP[i - coins[j]] + 1 } = min{ DP[i - coins[j]] } + 1

这里运用动态规划的思路解决该问题。按照一般思路，我们先从最基本的情况来一步一步地推导。

这里

我们先假设一个函数 d(i)d(i) 来表示需要凑出 ii 的总价值需要的最少硬币数量。

  • 当 i=0i = 0 时，很显然我们可以知道 d(0)=0d(0) = 0 。因为不要凑钱了嘛，当然也不需要任何硬币了。注意这是很重要的一步，其后所有的结果都从这一步延伸开来。
  • 当 i=1i = 1 时，因为我们有 1 元的硬币，所以直接在第 1 步的基础上，加上 1 个 1 元硬币，得出 d(1)=1d(1) = 1 。
  • 当 i=2i = 2 时，因为我们并没有 2 元的硬币，所以只能拿 1 元的硬币来凑。在第 2 步的基础上，加上 1 个 1 元硬币，得出 d(2)=2d(2) = 2 。
  • 当 i=3i = 3 时，我们可以在第 3 步的基础上加上 1 个 1 元硬币，得到 3 这个结果。但其实我们有 3 元硬币，所以这一步的最优结果不是建立在第 3 步的结果上得来的，而是应该建立在第 1 步上，加上 1 个 3 元硬币，得到 d(3)=1d(3) = 1 。 ...

接着就不再举例了，我们来分析一下。可以看出，除了第 1 步这个看似基本的公理外，其他往后的结果都是建立在它之前得到的某一步的最优解上，加上 1 个硬币得到。得出：

d(i)=d(j)+1d(i) = d(j) + 1

这里 j<ij < i 通俗地讲，我们需要凑出 ii 元，就在凑出 jj 的结果上再加上某一个硬币就行了。

那这里我们加上的是哪个硬币呢。嗯，其实很简单，把每个硬币试一下就行了：

  1. 假设最后加上的是 1 元硬币，那 d(i)=d(j)+1=d(i−1)+1d(i) = d(j) + 1 = d(i - 1) + 1 。
  2. 假设最后加上的是 3 元硬币，那 d(i)=d(j)+1=d(i−3)+1d(i) = d(j) + 1 = d(i - 3) + 1 。
  3. 假设最后加上的是 5 元硬币，那 d(i)=d(j)+1=d(i−5)+1d(i) = d(j) + 1 = d(i - 5) + 1 。

我们分别计算出 d(i−1)+1d(i - 1) + 1 , d(i−3)+1d(i - 3) + 1 , d(i−5)+1d(i - 5) + 1 的值，取其中的最小值，即为最优解，也就是 d(i)d(i) 。

最后公式：

d(i)=min(d(i−vx)+1)d(i) = min(d(i - v_x) + 1)（这里的 vxv_x 表示硬币的币值, i−vx≥0i-v_x \geq 0）

这里用 Java 实现了基本的代码：

public class CoinProblemBasicTest {

    private int[] d; // 储存结果
    private int[] coins = {1, 3, 5}; // 硬币种类

    private void d_func(int i, int num) {
        // 这步单纯就是初始化
        if (i == 0) {
            d[i] = 0;
            d_func(i + 1, num);
        }
        else {
            int min = 9999999; // 初始化一个很大的数值。当最后如果得出的结果是这个数时，说明凑不出来。
            // 遍历硬币
            for (int coin : coins) {
                if (i >= coin && d[i - coin] + 1 < min) {
                    min = d[i - coin] + 1;
                }
            }

            d[i] = min;

            // 这里的递归其实就是一个 for 循环
            // 它等价于这整个 else 的外层循环 for(int i = 1;i < num; i++)
            if (i < num) {
                d_func(i + 1, num);
            }
        }
    }


    @Test
    public void test() throws Exception {
        int sum = 11; // 需要凑 11 元
        d = new int[sum + 1]; // 初始化数组

        d_func(0, sum); // 计算需要凑出 0～sum 元需要的硬币数量
        for (int i = 0; i <= sum; i++) {
            System.out.println("凑齐 " + i + " 元需要 " + d[i] + " 个硬币");
        }
    }
}

结果如下：

凑齐 0 元需要 0 个硬币
凑齐 1 元需要 1 个硬币
凑齐 2 元需要 2 个硬币
凑齐 3 元需要 1 个硬币
凑齐 4 元需要 2 个硬币
凑齐 5 元需要 1 个硬币
凑齐 6 元需要 2 个硬币
凑齐 7 元需要 3 个硬币
凑齐 8 元需要 2 个硬币
凑齐 9 元需要 3 个硬币
凑齐 10 元需要 2 个硬币
凑齐 11 元需要 3 个硬币

动规和递归的关系​

TODO: 动态规划和递归之间的关系是什么？ - 大宽宽的回答 - 知乎 https://www.zhihu.com/question/410196236/answer/1380157269