KMP模式匹配算法

参考资料大话数据结构

什么是 KMP

KMP 是一种字符匹配算法，因为觉得对一些无规律的二进制数据进行匹配有启发，这里也将其记录下来，在学习这个算法之前先来看下朴素的匹配算法

朴素匹配算法

朴素匹配算法，又称为BF算法就如它的名字一样很简单，每次匹配逐个匹配，当匹配不成功就回到上次开始匹配的位置（主串）加一位继续重头开始匹配

public class App {
    public static void main(String[] args) throws Exception {
        char[] s = { '张', '三', '是', '个', '学', '生', '！' };
        char[] t = { '学', '生' };

        int i = 0; // 用来记录当前子串在主串的第几个字符
        int j = 0; // 用于子串中当前位置的下标值

        while (i < s.length && j < t.length) {
            if (s[i] == t[j]) {
                System.out.println(t[j]);
                j++;
                i++;
            } else {
                // 退回到上次匹配的位置
                i = i - j + 1; // 就是回退到开始匹配的那个字符的上一个位置
                j = 0;
            }
        }

        if (j > t.length - 1) {
            System.out.println("匹配成功，匹配的位置是" + (i - j + 1));
        } else {
            System.out.println("不存在");
        }
    }
}

如上所示，实际就是维护一个下标，每次匹配失败这个下标就归位，但是上述算法最好的情况是什么，那就是一开始就匹配成功，比如 “googlegood” 中去找 “google” ，时间复杂度为 O(1)

如下图所示：

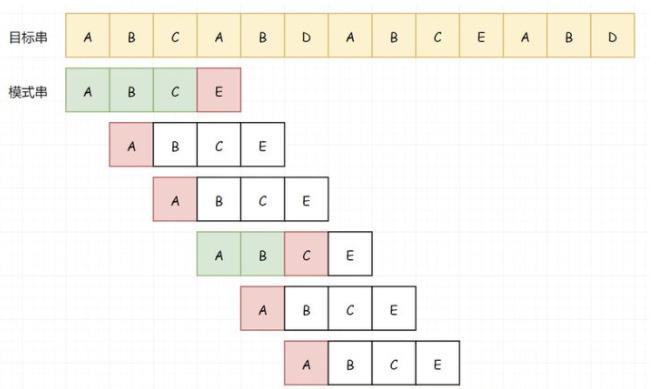
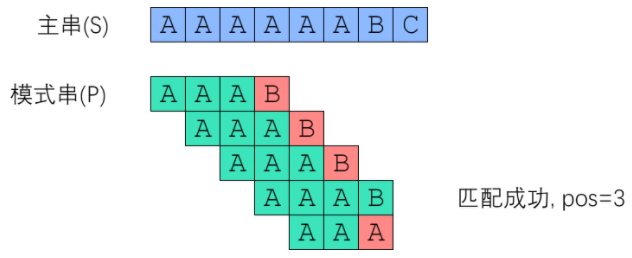
而最坏的情况就是每次不成功的匹配都位于串的最后一个字符，举个极端的例子：

S: 00000000000000000000000000000000001
T：0000001

那匹配时每次都需将 T 字符循环到最后一位才发现它们是不匹配的，因此最坏情况的时间复杂度为: $O((n - m + 1) * m)$

KMP 模式匹配算法

于是有三个大师 D.E.Knuth、J.H.Morris 和 V.R.Pratt 发表的一个模式匹配算法，KMP 算法就是对上述那种重复的情况进行的改进

KMP 就是对上面那种重复匹配的场景进行优化，举个例子：

S：abcdefg
T：abcx

对于子串 T 来说，“abcx” 首字母 “a” 不与后面的子串任意一字符相等，所以当匹配到 “x” 匹配失败之后，再回溯到 “b” 这样继续从 “a” 到 “x” 这样慢慢比较就没有意义了，因此得找个策略直接跳过这些一定不相同的情况

还有一种情况，就是子串内部也有和首字符一样的字符该如何处理：

S：abcababca
T：abcabx

这里 T 的首字符和第四位的 “a” 相等，第二位的 “b” 与第五位的 “b” 相等，但是在最开始比较时第四位的 “a” 和第五位的 “b” 已经与主串 S 中的相应位置比较过了，是相等的，因此可以断定：T 的首字符 “a”、第二位的字符 “b” 与 S 也不需要比较了，肯定也是相等的因为第一次已经比较过了，所以这里也可以跳过

正所谓好马不吃回头草，KMP 就是为了让没必要的回溯不发生，即上面的那个 i 是不可以变小的

既然 i 值不回溯，那要考虑的变化就是 j 的值了，而前面一直说的都是 T 串的首字符与自身后面字符的比较，发现如果有相等字符，j 值的变化就会不相同。也就是说这个 j值的变化与主串其实没有关系，关键就取决于 T 串的结构中是否有重复的问题

如下两个例子： 1、T=“abcdex”，当中没有任何重复的字符，所以 j 就由 5 变成 0（从 0 开始计），而 i 还是位于原位 2、T=“abcabx”，前缀的 “ab” 与最后 “x” 之前串的后缀 “ab” 是相等的，因此 j 就由 5 变成了 2，这样就可以从 i 的后两位开始比较（因为有重复的，所以可以直接跳过）

因此可以得出规律，j 值的多少取决于当前字符之前的串的前后缀的相似度，从而把 T 串各个位置的 j 值的变化定义为一个数组 next，那么 next 的长度就是 T 串的长度

下面来看下这个 next 数组是怎么推导的

next 数组值推导

参考资料 KMP的next数组求法详解参考资料如何更好地理解和掌握 KMP 算法? - 灵茶山艾府的回答

先来看下什么是前缀后缀：

真前缀指除了最后一个字符外，一个字符串的全部头部组合
真后缀指除了第一个字符以外，一个字符串的全部尾部组合

如下例子（前缀是包括第一个或最后一个的，但是一般只使用真前缀）：

abcdef的真前缀：a、ab、abc、abcd、abcde（注意：abcdef不是真前缀）
abcdef的真后缀：f、ef、def、cdef、bcdef（注意：abcdef不是真后缀）
abcdef的公共最大长：0（因为其前缀与后缀没有相同的）
ababa的真前缀：a、ab、aba、abab
ababa的真后缀：a、ba、aba、baba
ababa的公共最大长：3（因为他们的公共前缀后缀中最长的为aba，长度3）

KMP 算法的精髓就在于 next 数组，通过它来达到跳跃式匹配的高效模式，这个 next 数组的值是代表着字符串的 前缀和后缀相同的最大长度（不包括自身）

这里举个例子：

这样我们就求出来了next数组：

当前后缀特别长的时候（假设该串大小为 1000），我们当然不可能挨个去比较前后缀，next 数组怎样用代码去求呢？

所以这里看下面的例子：

列个表手算一下：（最大匹配数为子字符串 [0...i] 的最长匹配的长度）

子字符串　 a b a b a b z a b a b a b a
最大匹配数 0 0 1 2 3 4 0 1 2 3 4 5 6 ?

一直算到 6 都很容易。在往下算之前，先回顾下我们所做的工作：

对子字符串 abababzababab 来说，

真前缀有 a, ab, aba, abab, ababa, ababab, abababz, ...

真后缀有 b, ab, bab, abab, babab, ababab, zababab, ...

所以子字符串 abababzababab 的真前缀和真后缀最大匹配了 6 个（ababab），那次大匹配了多少呢？容易看出次大匹配了 4 个（abab），更仔细地观察可以发现，次大匹配必定在最大匹配 ababab 中，所以次大匹配数就是 ababab 的最大匹配数！

直接去查算出的表，可以得出该值为 4

第三大的匹配数同理，它既然比 4 要小，那真前缀和真后缀也只能在 abab 中找，即 abab 的最大匹配数，查表可得该值为 2

再往下就没有更短的匹配了。

回顾完毕，来计算 ? 的值：既然末尾字母不是 z，那么就不能直接 6+1=7 了，我们回退到次大匹配 abab，刚好 abab 之后的 a 与末尾的 a 匹配，所以 ? 处的最大匹配数为 5

上 Java 代码，它已经呼之欲出了：

// 构造模式串 pattern 的最大匹配数表
int[] calculateMaxMatchLengths(String pattern) {
    int[] maxMatchLengths = new int[pattern.length()];
    int maxLength = 0;

    for (int i = 1; i < pattern.length(); i++) {
        while (maxLength > 0 && pattern.charAt(maxLength) != pattern.charAt(i)) {
            maxLength = maxMatchLengths[maxLength - 1]; // <1>
        }

        if (pattern.charAt(maxLength) == pattern.charAt(i)) {
            maxLength++; // <2>
        }

        maxMatchLengths[i] = maxLength;
    }
    return maxMatchLengths;
}

有了代码后，容易证明它的复杂度是线性的（即运算时间与模式串 pattern 的长度是线性关系）：

由 ② 可以看出 maxLength 在整个 for 循环中最多增加 pattern.length() - 1 次
让 maxLength 减少的 ① 在整个 for 循环中最多会执行 pattern.length() - 1 次

从而 calculateMaxMatchLengths 的复杂度是线性的。

KMP 匹配的过程和求最大匹配数的过程类似，从 count 值的增减容易看出它也是线性复杂度的：

// 在文本 text 中寻找模式串 pattern，返回所有匹配的位置开头
List<Integer> search(String text, String pattern) {
    List<Integer> positions = new ArrayList<>(); // 用于存储匹配到的位置
    int[] maxMatchLengths = calculateMaxMatchLengths(pattern);
    int count = 0; // 等价与上面朴素算法的 j

    for (int i = 0; i < text.length(); i++) {
        while (count > 0 && pattern.charAt(count) != text.charAt(i)) {
            count = maxMatchLengths[count - 1];
        }

        if (pattern.charAt(count) == text.charAt(i)) {
            count++;
        }

        if (count == pattern.length()) {
            positions.add(i - pattern.length() + 1);
            count = maxMatchLengths[count - 1];
        }
    }

    return positions;
}

什么是 KMP​

朴素匹配算法​

KMP 模式匹配算法​

next 数组值推导​

什么是 KMP

朴素匹配算法

KMP 模式匹配算法

next 数组值推导